ELEXPO EVOLUTION

 

Teoria dei Giochi per l'Elexpo

Utilizzando il tema del film " A Beautiful Mind" come una metafora o come una fonte d'ispirazione, esso vale come suggerimento per interpretare la Navigazione nella Rete della Vita nel contesto della teoria dei giochi.

•Nel modello della "Teoria dei Giochi", tutti devono essere a conoscenza delle regole del gioco, ed essere consapevoli delle conseguenze di ogni singola mossa. La mossa, o l'insieme delle mosse, che un individuo intende fare viene chiamata " strategia". In dipendenza dalle strategie adottate da tutti i giocatori (o agenti), ognuno riceve un "pay-off" ( il "pagamento d'uscita", o vincita finale,  secondo un'adeguata unità di misura) che può essere positivo, negativo o nullo.
 

La teoria dei giochi si presenta all'Elexpo come la disciplina che si occupa di situazioni di interazione strategica fra utenti decisori,  giocatori usualmente assunti essere “intelligenti” e “razionali”. “Intelligenti” significa che capiscono la situazione in cui si trovano e sono in grado di fare ragionamenti logici complessi. “Razionali” significa che hanno preferenze sulle conseguenze del processo decisionale e che hanno l’obiettivo di ottimizzare l’utilità di queste conseguenze. A tale scopo ogni utente (giocatore) ha una sua “funzione di utilità” definita sull’insieme degli esiti del gioco.

 In generale, un gioco è caratterizzato da :

·         Un insieme di giocatori  i = 1, 2, . . . , n ciascuno dei quali sceglie quale strategia adottare nell’insieme Si.

·         Il vettore S = (s1, s2, . . . , sn) delle strategie adottate dai giocatori

·         Il vettore C = (c1,c2, . . . , cn) delle conseguenze delle strategie

·         Il vettore U = (u(c1)),u(c2), . . . ,u(cn)) delle utilità delle conseguenze..

"No, non credo alla fortuna. Credo all’importanza di dare un valore alle cose”. (J.Nash)

La teoria dei giochi presume che una persona intelligente e razionale possa attribuire una valutazione numerica  ad ogni cosa e se ne serva per decidere il miglior corso d’azione.

Questo numero associato all'utilità delle conseguenze lo chiamiamo 'Utilità per l'Elexpo'.

Quindi lo scopo dell’Elexpo intelligente e razionale è scegliere una strategia d ’azione che generi una conseguenza utile, cioè capace di soddisfare  l'aspettativa  e ottimizzare l'utilità.

 

A Beautiful Mind per l'Elexpo

Ci sono parti in conflitto che desiderano trovare un accordo di cooperazione per gestire al meglio le loro divergenze. Si può fornire loro un suggerimento adeguato per risolvere il conflitto in modo ragionevole ? Ad esempio se due ragazzi sono impegnati nel corteggiamento di alcune ragazze, possiamo aiutarli a cogliere gli aspetti salienti del conflitto e fornire loro un criterio generale per comporlo ? Quindi come possiamo descrivere un problema di contrattazione e che tipo di soluzione possiamo suggerire ?



Guarda la scena del film


La scena del film "A Beautiful Mind" maggiormente citata in relazione alla teoria dei giochi mostra Nash intento a suggerire a quattro amici come organizzare il corteggiamento di cinque ragazze, una delle quali è bionda e molto più attraente delle altre quattro, che sono more.

Nella scena del film i giocatori sono cinque: Nash e i suoi quattro amici. Ognuno di essi ha la stessa funzione di utilità, che attribuisce valore “a” alla conquista della bionda, “b” a per una qualsiasi delle more e “c” ad essere respinto, con a > b > c. Ognuno di essi può adottare come strategia di corteggiare una qualsiasi delle cinque ragazze, ma il successo è garantito soltanto se il corteggiamento non è insidiato da un rivale. A chi dovrebbero rivolgere la loro attenzione i giocatori? 

L’ovvia risposta è che sarebbe opportuno che ciascuno dei cinque corteggiasse una  ragazza diversa. Come spiega lucidamente Nash, in questo modo nessuno intralcia gli altri e i cinque amici possono congiuntamente conseguire l’utilità ottima, cioè la massima utilità possibile per il gruppo.

Questa proposta di soluzione del problema del corteggiamento è nota in economia come  ottimo paretiano. Una scelta di gioco  "S"  è un ottimo paretiano se non esiste nessun altra scelta "S’" che sia più utile per il gruppo. Giocare congiuntamente un ottimo paretiano significa evitare di sprecare utilità e dunque risulta molto naturale  suggerire di guidare l’azione sociale verso un ottimo paretiano. 

 

Semplifichiamo il gioco al caso di due giocatori e supponiamo che due agenti in conflitto - che chiameremo Nash e Martin - abbiano aperto un negoziato per decidere come corteggiare 3 ragazze, di cui 2 more ed 1 una bionda, più carina delle altre.

 In generale, un negoziato tra due giocatori è caratterizzato da :

Diciamo  quindi che la terna (C,P,U) definisce un problema di contrattazione.

 

Rappresentiamo il Gioco nel contesto dei data base :

Schema delle Relazioni tra le Entità





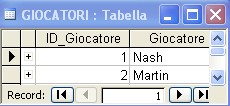
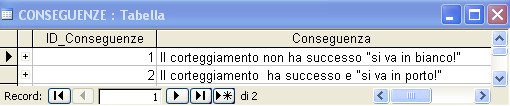
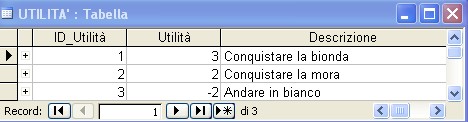
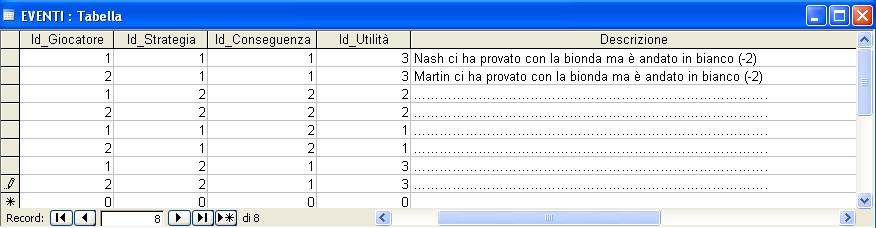
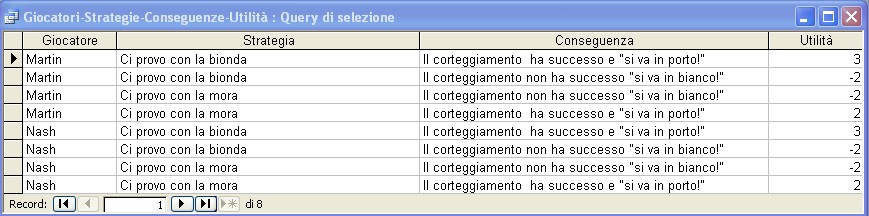
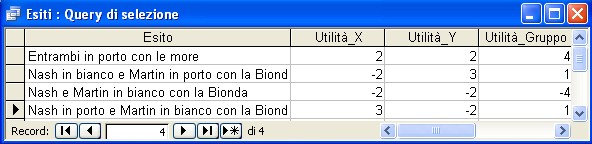
Interrogando la base di dati U-DBMS risulta che gli eventi (esiti) possibili sono  4:

Rappresentiamo le 4 coppie di utilità attese come punti nel seguente spazio cartesiano, dove l'asse x rappresenta le utilità attese, cioè le aspettative,  di Nash, mentre l'asse y quelle di Martin.

La coppia (x,y) identifica l'utilità di (Nash,Martin), sappiamo che entrambi attribuiscono valore a=3 : sedurre la bionda, b=2 : sedurre la mora, c=-2 : ricevere il "due di picche".

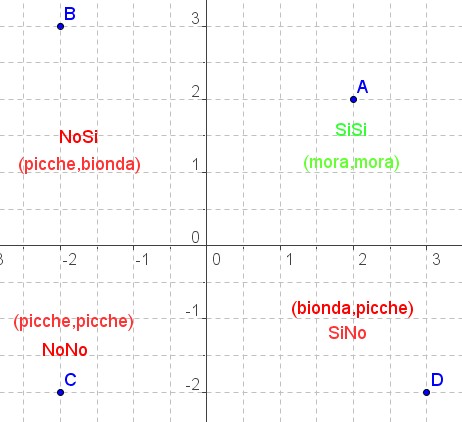
Utilità per il singolo

 

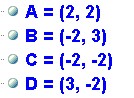
Utilità per il singolo e per il  gruppo

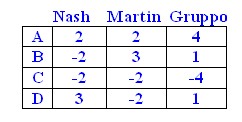
Rappresentazione qualitativa  dell'utilità mediante funzioni continue

Andamento delle funzioni di utilità (U) :  interna (x) , esterna(y) , globale(x+y)

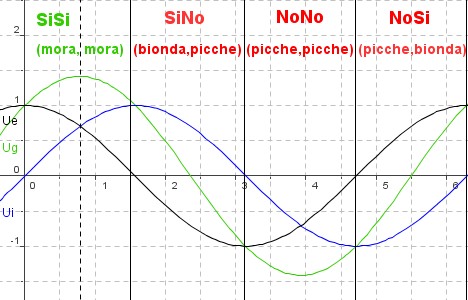
La retta verticale tratteggiata individua la situazione migliore per il gruppo.
Ottimo Paretiano

Significato del Grafico delle Utilità

Lo spostamento lungo l'asse orizzontale corrisponde alla modulazione della qualità della relazione (o connessione) tra rete interna e rete esterna. Si parte dalla regione SiSi : nel punto 0 si ha utilità interna nulla e utilità esterna massima (Ui=0 e Ue=1), poi muovendo verso destra si assiste ad un progressivo aumento dell'utilità interna e ad una contemporanea riduzione dell'utilità esterna,in corrispondenza della linea tratteggiata verticale si ha la situazione in cui i due valori sono uguali, questo punto corrisponde all'ottimo paretiano, cioè alla situazione in cui la somma delle utilità Ui e Ue assume il valore  massimo possibile. Superato questo punto l'utilità interna continua ad aumentare e quella esterna a diminuire fino al punto in cui la prima è al massimo e la seconda a zero. A questo punto si entra nella regione SiNo dove l'utilità interna inizia a diminuire pur rimanendo positiva, mentre quella esterna diventa sempre più negativa. Continuando si arriva al limite in cui l'utilità interna è nulla mentre quella esterna è al minimo possibile. Proseguendo si entra nella regione NoNo dove l'utilità interna diminuisce diventando sempre più negativa mentre l'utilità esterna aumenta pur rimanendo sempre negativa. Superata questa regione dell'estrema criticità si entra nella regione NoSi dove l'utilità interna aumenta pur rimanendo negativa mentre quella esterna diventa sempre più positiva, giunti al limite in cui l'utilità interna è nulla mentre quella esterna è massima, il ciclo si compie e si ritorna nella regione SiSi.

 

Morale della Metafora per l'Elexpo

•L'equilibrio di Nash rappresenta una situazione nella quale il gruppo si viene a trovare se ogni componente del gruppo fa ciò che è meglio per sé, cioè mira a massimizzare il proprio profitto a prescindere dalle scelte degli avversari. Tuttavia, non è detto che l'equilibrio di Nash sia la situazione migliore per tutti, per il Noi. Infatti, è possibile che un gruppo di giocatori, o, al limite, tutti, possano aumentare il proprio guadagno allontanandosi di comune accordo dall'equilibrio di nash.

Quindi per ottenere il massimo guadagno per il gruppo è necessario che si instauri una cooperazione tra i giocatori, vale a dire che tutti agiscano non col fine di ottenere solo il miglior risultato per sé, ma di ottenere il miglior risultato per il gruppo, e quindi, indirettamente, ottenendo un risultato migliore anche per sé.

•Quindi l'equilibrio di Nash non è la soluzione migliore per tutti.
•È noto infatti che l'equilibrio di Nash può non essere un “ottimo di Pareto”, e quindi possano esistere altre combinazioni di strategie che conducono a migliorare il guadagno di alcuni senza ridurre il guadagno di nessuno, o addirittura (come accade nel caso del dilemma del prigioniero) ad aumentare il guadagno di tutti.

Tuttavia spesso la razionalità collettiva (ciò che sarebbe meglio per il gruppo) contrasta con quella individuale (ciò che sarebbe meglio per me), e poiché l’egoismo spesso prevale sull’altruismo,  nella maggior parte dei casi necessario un accordo vincolante tra i giocatori (e quindi una istituzione che vigili su tale accordo) ed una sanzione nei confronti di chi non lo rispetta.

•In questo modo si riduce il profitto del singolo se esso si allontana dalle strategie che garantiscono al gruppo il miglior risultato, e ciò affinché nessuno ’accordo di cooperazione.
 

Generalizzazione per l'Elexpo

Quella che abbiamo appena visto è un interpretazione dell’andamento dei negoziati tra due parti che si conserva vera su molte scale, a prescindere da quali siano i casi particolari presi in esame. L’invarianza di scala sta a significare che uno stesso schema di organizzazione si manifesta su scale diverse.

Quindi questa  rappresentazione particolare del problema del corteggiamento, può essere generalizzata nel seguente

"Spazio delle Connessioni Possibili"
o
(Spazio delle Fasi del Sistema)

 

Il quale può essere modulato ed interpretato in una molteplicità di livelli di gioco

Modello di organizzazione che interessa tutti i livelli della rete della vita.

 

A Beautiful World per l'Elexpo

Reinterpretiamo il tema nel livello di gioco che vede coinvolti l'Uomo e il Pianeta Terra.
Indichiamo con "U=(X,Y)" il vettore delle funzioni di utilità dei due giocatori.

X = {x=2 : aspettativa positiva del Client Uomo (Soddisfare i propri bisogni)

         x =-2: aspettativa negativa del Client Uomo (Delusione dei propri bisogni )}

Y = {y=2  : aspettativa positiva del Client Pianeta  (Rispetto e atteggiamenti sostenibili)

         y =-2: aspettativa negativa del Client Pianeta (Sfruttamento indiscriminato delle risorse)}

Le strategie di gioco possibili sono descritte da due classi di caratteristiche (connessioni) :

Connessione del Si : Coerenza e Reciproco Sostegno tra Uomo e Pianeta

o      (SI , SI) : (Mi sostengo,Ti sostengo) : Agire e soddisfare i bisogni di entrambi  

 

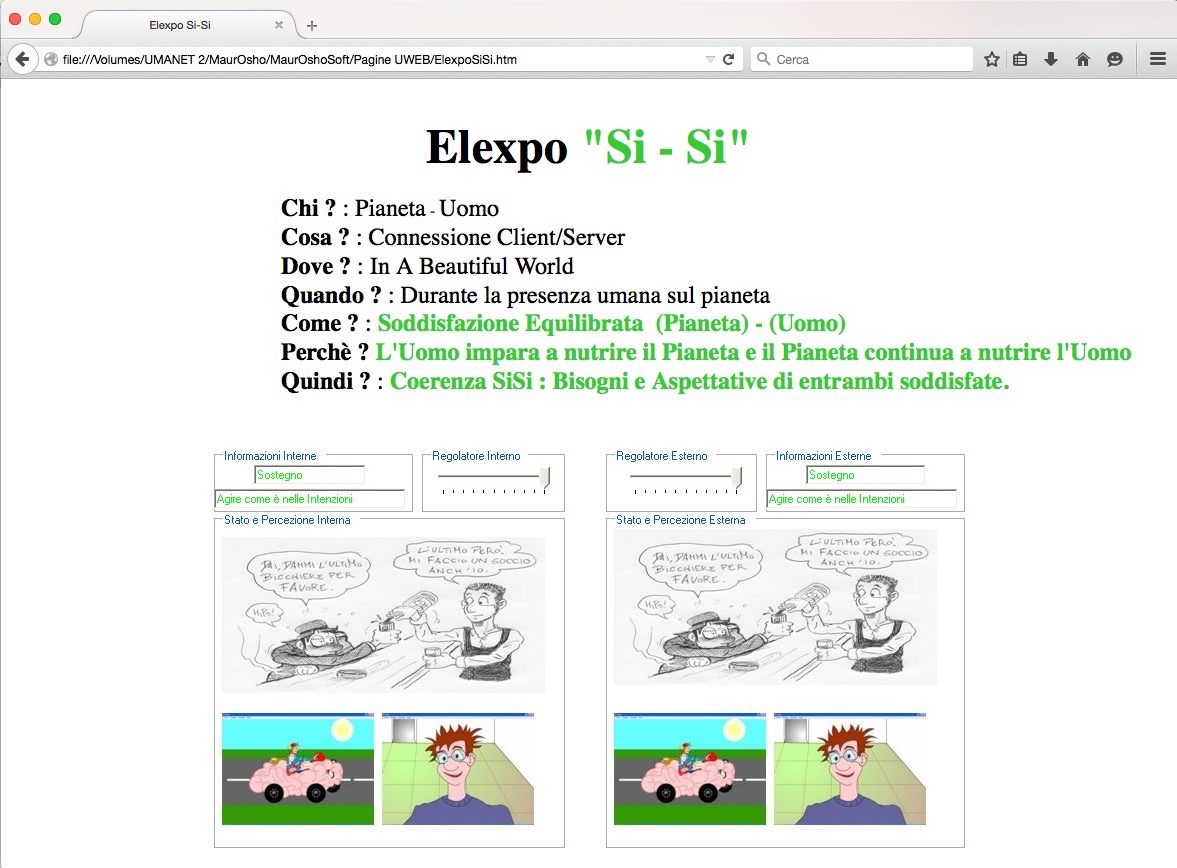
Connessione del No : Paradosso e Oppressione tra Uomo e Pianeta

o      (Si , No) : (Mi Sostengo, Ti Opprimo) : Uomo soddisfatto, Pianeta deluso

 

o      (No , Si) : (Mi Opprimi , Ti Sostieni) : Uomo deluso, Pianeta soddisfatto

 

o      (No , No) : (Mi Opprimi , Ti Opprimo) : Entrambi delusi

 

  Morale della Navigazione dell'Elexpo

Potenziale Elexpo per cambiare la realtà anzichè puntare il dito contro qualcuno, inizia a cambiare te stesso. Non cercare di cambiare la realtà esterna è impossibile cerca invece di fare l'unica cosa saggia: giungere alla verità. Quale verità ? Che la realtà non esiste allora ti accorgerai che non è la realtà a cambiare ma sei tu stesso. Trasformando te stesso potrai equilibrare l'anomalia Iper/Ipo e ripristinare il codice dell'Equilibrio. Sviluppando consapevolezza imparerai a "Svuotare il Troppo Pieno e Riempire il Troppo Vuoto": ridurre ciò che è eccessivio ed aumentare ciò che è carente.

Guarda la cronologia dei tuoi comportamenti e valuta dove sei stato Troppo (...) e Troppo poco (...) 
  Correggi l'anomalia iper/ipo terminando il caricamento delle pagine tramite la Connessione del No
  Ripensa  il tuo comportamento e fai un passo indietro verso Equilibrio (...)(...) 
 Ritorna al centro e collegati tramite la Connessione del Si: Mi Sostengo/Ti Sostengo

 

.


L'Elexpo fa il download dell'utilità ottima per il gruppo

Il potenziale Elexpo al termine di questo percorso ha compreso che nel Gioco della Navigazione nella Rete della Vita ci sono 4 possibili pattern di relazione (connessioni) tra lui e l'ambiente esterno, sia esso un amico, un insegnante o il pianeta.
Nel gioco della relazione può accadere che qualcuno rimanga deluso, l'Elexpo in queste situazioni analizza i Paradossi Iper/Ipo, interrogandosi su come agire per ripristinare l'equilibrio.

Come nel problema del corteggiamento, anche nella vita la competizione non sempre conduce al miglior risultato. La cooperazione permette di aumentare l'utilità di tutti. Il compito dell'Elexpo, quando interagisce con l'ambiente, è quello di scegliere la strategia che conduce all'Ottimo di Pareto. Una situazione di reciproco sostegno in cui tutti vincono.

L'Elexpo la chiama Connessione SiSi: Reciproco Sostegno tra Uomo e Ambiente.